How To Draw Slope Fields For Differential Equations

Differential Equation 2 – S lope Fields

Of course, we always want to see the graph of an equation we are studying. The graph of a differential equation is a slope field.  A offset derivative expressed equally a part of 10 and y gives the slope of the tangent line to the solution curve that goes through any point in the plane.

Slope fields make use of this past imposing a filigree of points evenly spaced across the Cartesian plane. At each bespeak the value of the derivative is calculated and a short segment with that slope is drawn. These segments graphed together form the slope field.

Here is the gradient field for the differential equation

A good way to introduce slope fields to your class is to put or projection a coordinate system on the board. Give each student 1 or 2 points (i, –3), (one, –2), (1, –1), (1, 1), (one, 2), etc. Have them summate the derivative at their point(southward) so come up to the board and draw a brusque segment through their betoken(due south) with the slope they calculated. The result will be a slope field.  (This is, in fact, a common costless-response question on the AP exams. Students are given a graph with 9 – 12 points plotted and they are asked to apply them to draw a slope field for a given differential equation.)

The big thought with slope fields is to use them to get an idea of what the solutions look like, peculiarly if the differential equation cannot be solved.  The solutions are lurking in the gradient field. What do they look similar in the figure? Circles of grade. We solved this differential equation in the concluding post. The general solution is . Of form they are not all that simple.

Since the solution graphs are lurking in the slope field, the adjacent matter to do is to use the slope field to sketch a item solution.  After plotting the initial condition (a signal) students should draw a curve through the point that follows the slope field from border to edge in both directions.

In the previous post (instance 2) we found the item solution of with the initial status point (4, –3) to be . This is shown drawn on the slope field in the next graph. The black dot is the signal (4, –3). Notice how the solution graph follows the slope field, simply does not necessarily hit whatever of the segments. The solution will touch a segment only if the midpoint of the segment happens to be on the solution – this is non usually the case.

Slope fields are tedious and fourth dimension-consuming to describe past mitt. It's a job for computers. At that place are various graphing computer programs available on the net. Computer screen are non the all-time for seeing gradient fields; they are as well small and you should be certain to e'er be in a square window (or the slopes volition not look correct).

At that place are many websites that will describe slope fields and solution curves for you.  You tin can attempt this ane. The figures in this post were done with Winplot (of class, my favorite). The good ones permit you draw and breathing solution curves over the slope field. (I have not establish a good slope field generator app for iPads; if anyone makes apps, consider this a hint.)

Here is a brief example that shows how powerful an animated graph can exist. In Winplot, follow the path Window > 2-dim > Equa > differential > dy/dx.  Enter the differential equation in the box and accommodate the other settings every bit necessary.  Exist sure yous are in a square window (CTRL+Q).

The example below is from the 2002 BC exam question 5: . Detect that this equation is non separable; students were not expected to solve it. They were asked to depict the solution curves through the two points (0, 1) and (0, –ane) shown here in blue. These points are marked on the graph (Equa > point > (x,y)). The full general solution, establish by CAS, is . Enter this (Equa > i.Explicit) and open the C slider (Anim > individual > C).

In the video below the C values go from –v to five. They terminate momentarily at the two initial condition points (C = –two for (0,–1) and C = 0 for (0, ane)). These are what the students were expected to sketch.

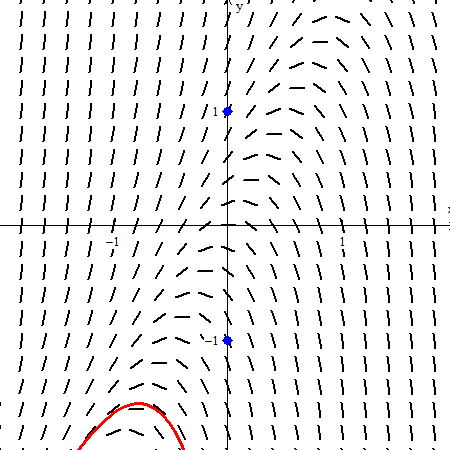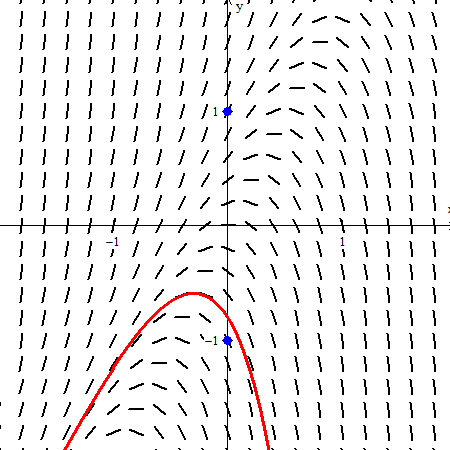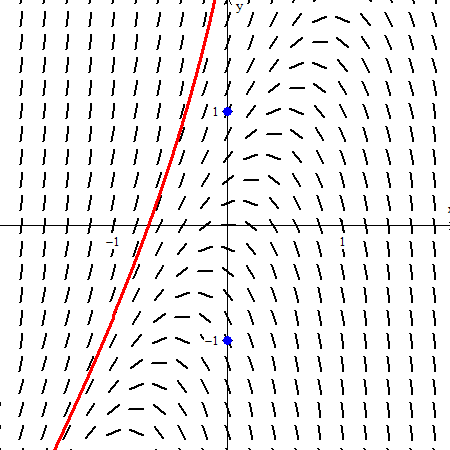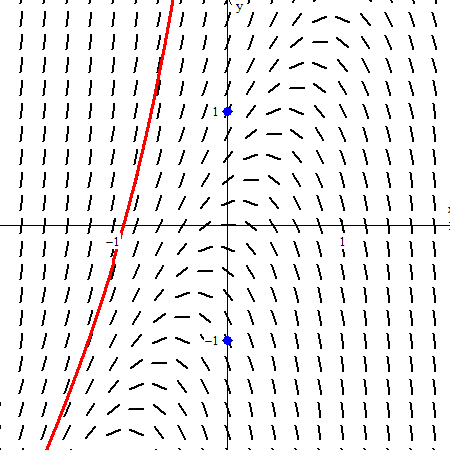
The point is to encounter how the different values of C effect the equation, each giving its ain particular solution, and to see the different solution hiding in the slope field.

Source: https://teachingcalculus.com/2015/01/09/slope-fields/

Posted by: troupeingthe.blogspot.com

Share this post