how to draw a normal distribution curve

Probability and Statistics > Normal Distributions

Contents:

1. What is a Normal distribution?
2. The Standard Normal Model
3. Normal Distribution Discussion Problems.
4. Normal Distribution on the TI 89 Examples
5. Excel Graph Instructions
6. Probability Density Function
7. Related Articles.

What is a Normal distribution?

Lookout the video for an overview of the normal distribution:

Can't encounter the video? Click here.

A normal distribution.

A normal distribution, sometimes called the bell bend, is a distribution that occurs naturally in many situations. For case, the bong curve is seen in tests similar the SAT and GRE. The majority of students will score the boilerplate (C), while smaller numbers of students will score a B or D. An even smaller percent of students score an F or an A. This creates a distribution that resembles a bell (hence the nickname). The bell curve is symmetrical. Half of the data will fall to the left of the mean; half will fall to the right.
Many groups follow this type of pattern. That'due south why it'southward widely used in business, statistics and in regime bodies like the FDA:

• Heights of people.
• Measurement errors.
• Blood pressure.
• Points on a test.
• IQ scores.
• Salaries.

The standard deviation controls the spread of the distribution. A smaller standard deviation indicates that the information is tightly clustered around the mean; the normal distribution will be taller. A larger standard deviation indicates that the data is spread out around the mean; the normal distribution will be flatter and wider.

Properties of a normal distribution

• The hateful, fashion and median are all equal.
• The bend is symmetric at the center (i.eastward. around the mean, μ).
• Exactly half of the values are to the left of center and exactly half the values are to the right.
• The full area under the curve is 1.

The Standard Normal Model
A standard normal model is a normal distribution with a mean of 0 and a standard deviation of 1.

Standard Normal Model: Distribution of Data

One mode of figuring out how information are distributed is to plot them in a graph. If the data is evenly distributed, yous may come up with a bell bend. A bell bend has a modest percentage of the points on both tails and the bigger percent on the inner part of the curve. In the standard normal model, nearly 5 percent of your data would fall into the "tails" (colored darker orangish in the image below) and 90 percentage will be in between. For case, for exam scores of students, the normal distribution would show 2.5 percent of students getting very low scores and 2.five percent getting very high scores. The residual will exist in the middle; not also high or too low. The shape of the standard normal distribution looks like this:

Practical Applications of the Standard Normal Model

The standard normal distribution could aid you figure out which subject you are getting expert grades in and which subjects you lot have to exert more endeavor into due to low scoring percentages. Once you become a score in one subject that is higher than your score in some other subject area, y'all might think that you are better in the subject area where yous got the college score. This is not always true.

Yous tin simply say that you are better in a detail subject if y'all get a score with a certain number of standard deviations above the mean. The standard deviation tells you how tightly your information is amassed around the hateful; Information technology allows y'all to compare different distributions that have unlike types of data — including different means.

For example, if y'all get a score of 90 in Math and 95 in English, you might think that you are amend in English than in Math. All the same, in Math, your score is ii standard deviations above the mean. In English, it's merely 1 standard divergence above the mean. It tells you that in Math, your score is far higher than most of the students (your score falls into the tail).
Based on this data, you really performed better in Math than in English!

Probability Questions using the Standard Model

Questions about standard normal distribution probability can look alarming just the key to solving them is understanding what the area under a standard normal curve represents. The total surface area under a standard normal distribution curve is 100% (that'due south "1" equally a decimal). For case, the left one-half of the curve is 50%, or .5. And then the probability of a random variable actualization in the left half of the curve is .5.

Of course, not all problems are quite that unproblematic, which is why there's a z-tabular array. All a z-table does is measure those probabilities (i.e. 50%) and put them in standard deviations from the mean. The mean is in the middle of the standard normal distribution, and a probability of fifty% equals zero standard deviations.

Standard normal distribution: How to Find Probability (Steps)

Stride 1: Draw a bell curve and shade in the area that is asked for in the question. The example below shows z >-0.8. That means y'all are looking for the probability that z is greater than -0.eight, and then you need to depict a vertical line at -0.8 standard deviations from the hateful and shade everything that'south greater than that number.

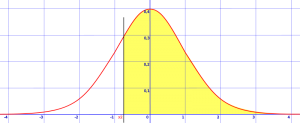
shaded area is z > -0.eight

Step two: Visit the normal probability area alphabetize and notice a film that looks like your graph. Follow the instructions on that folio to find the z-value for the graph. The z-value is the probability.

Tip: Step 1 is technically optional, but it'due south e'er a skillful idea to sketch a graph when you're trying to answer probability word problems. That's because most mistakes happen non because you can't do the math or read a z-table, only because yous subtract a z-score instead of adding (i.e. you imagine the probability under the curve in the wrong management. A sketch helps you cement in your caput exactly what y'all are looking for.

Normal Distribution Discussion Problems

This video shows 1 case of a normal distribution word problem.

Can't run across the video? Click here.

When you tackle normal distribution in a statistics class, you lot're trying to find the area under the curve. The full area is 100% (as a decimal, that's one). Normal distribution problems come in half dozen basic types. How do y'all know that a word trouble involves normal distribution? Look for the key phrase "assume the variable is normally distributed" or "assume the variable is approximately normal." To solve a word problem you need to effigy out which blazon you have.

1. "Between": Comprise the phrase "betwixt" and includes an upper limit and lower limit (i.e. "find the number of houses priced between $50K and 200K").
2. "More" or "Above": contain the phrase "more than than" or "above".
3. "Less Than".
4. Lower Cut Off Example (video)

ane. "Betwixt"

This how-to covers solving problems that comprise the phrase "between" and includes an upper and lower limit (i.e. "find the number of houses priced between $50K and 200K". Note that this is different from finding the "middle percentage" of something.

Word problems with normal distribution: "Between": Steps

Footstep 1: Identify the parts of the word problem. The word problem volition identify:

1. The hateful (average or μ).
2. Standard difference (σ).
3. Number selected (i.e. "cull ane at random" or "select ten at random").
4. X: the numbers associated with "between" (i.due east. "between $five,000 and $ten,000" would have 10 every bit v,000 and as $x,000).

In improver, y'all will be given EITHER:

1. Sample size (i.due east. 400 houses, 33 people, 99 factories, 378 plumbers etc.). OR
2. You might be asked for a probability (in which case your sample size will virtually likely be anybody, i.east. "Journeyman plumbers" or "Showtime year pilots."

Step 2: Depict a graph. Put the mean you identified in Footstep 1 in the center. Put the number associated with "between" on the graph (take a guess at where the numbers would fall–it doesn't take to be exact). For example, if your mean was $100, and you were asked for "hourly wages betwixt $75 and $125") your graph will expect something like this:

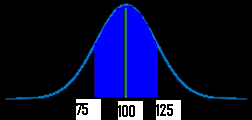
Step 3: Figure out the z-scores. Plug the first 10 value (in my graph higher up, information technology's 75) into the z value formula and solve. The μ (the hateful), is 100 from the sample graph. You can get these figures (including σ, the standard deviation) from your answers in step 1 :

*Note: if the formula confuses you, all this formula is request you to do is:
1. subtract the mean from X
2. split up by the standard difference.

Footstep four: Repeat footstep three for the second X.

Stride 5: Take the numbers from step 3 and 4 and use them to find the surface area in the z-table .

If you were asked to find a probability in your question, get to step 6a. If you were asked to find a number from a specific given sample size, go to step 6b.

Stride 6a:

Convert the answer from step five into a percent.

For example, 0.1293 is 12.93%.

That's it–skip step 6b!

Step 6b

Multiply the sample size (found in step 1) by the z-value you institute in step 4 . For example, 0.300 * 100 = xxx.

That's it!

2. "More than" or "In a higher place"

This how-to covers solving normal distribution problems that contain the phrase "more than than" (or a phrase like "to a higher place").

Step 1: Break upward the word problem into parts. Find:

1. The mean (average or μ)
2. Standard deviation (σ)
3. A number (for example, "choose l at random" or "select ninety at random")
4. Ten: the number associated with the "less than" statement. For example, if you were asked to detect "under $9,999" then X is nine,999.

Step 2: Find the sample from the trouble. You'll have either a specific size (like "chiliad televisions") or a general sample ("Every television").

Draw a film if the problem with the mean and the area you are looking for. For case, if the mean is $15, and you were asked to find what dinners cost more than $10, your graph might look like this:

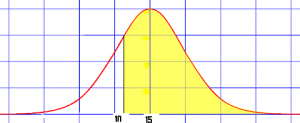
Step three: Calculate the z-score (plug your values into the z value formula and solve). Use your answers from footstep one :

Basically, all you are doing with the formula is subtracting the mean from X and so dividing that answer by the standard difference.

Step 4: Find the area using the z-score from step iii. Utilize the z-table . Not sure how to read a z-table? See the video on the z-tabular array page.

Step half-dozen: Go to Step 6a to detect a probability OR get to stride 6b to calculate a sure number or corporeality.

Stride 6a
Turn step 5's answer into a percentage.

For instance, 0.1293 is 12.93%.

Skip footstep 6b: you're done!

Step 6b
Multiply the sample size from Stride one past the z-score from footstep four . For example, 0.500 * 100 = 50.

You're done!

3. Less Than

This how-to covers solving normal distribution word problems that have the phrase "less than" (or a like phrase such as "fewer than").

Normal distribution word problems less than: Steps

Step 1: Pause upwardly the word problem into parts:

1. The mean (average or μ)
2. Standard deviation (σ)
3. Number selected (i.e. "choose one at random" or "select ten at random")
4. 10: the number that goes with "less than" (i.due east. "under $99,000" would list Ten equally 99,000)

Plus, yous will have EITHER:

1. A specific sample size. For example, 500 boats, 250 sandwiches, 100 televisions etc.
2. Everyone in the sample (y'all'll exist asked to discover a probability). For example "first twelvemonth medical students," "Cancer patients" or "Airline pilots."

Pace 2: Draw a pic to help you lot visualize the problem. The following graph shows a mean of xv, and an area "nether four"):

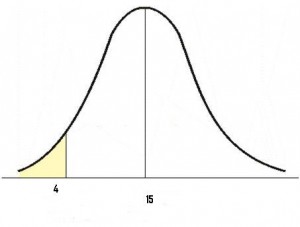
Footstep iii: Find the z value by plugging the given values into the formula. The "X" in our sample graph is four, and the μ (or hateful) is 15. You tin get these figures (including σ, the standard divergence) from your answers in stride 1, where you identified the parts of the problem:

All yous have to practise to solve the formula is:

1. Decrease the mean from 10.
2. Divide past the standard deviation.

Step 4: Have the number from stride 3, so use the z-table to notice the area.

Step v: To detect a probability, go to step 6a. To observe a number from a specific given sample size, go to pace 6b.

Step 6a

Alter the number from step 5 into per centum.

For example, 0.1293 is 12.93%.

That's it!

Step 6b

Multiply the sample size (establish in step i) past the z-value you institute in step 4 . For example, 0.300 * 100 = 30.

That's it!

4. Lower Cutting Off

Sometimes on a normal distribution word problem you'll exist asked to notice a "lower limit of an upper percent" of something (i.e. "find the cut-off point to pass a certain exam where the upper 40% of test takers pass"). A lower cut off point is the betoken where scores volition fall below that betoken. For instance, you might want to find where the cutting off betoken is for the lesser 10% of test takers.

Watch the video for an example:

Tin't see the video? Click hither.

Check out our YouTube channel for more worked issues.

Normal Distribution TI 89 Examples

In elementary statistics, you'll oft be faced with a question that asks y'all the cut off points for a sure percentage of the normal distribution, similar the top 90% or the top 10%. While working out these types of issues by hand is cumbersome, the TI-89 graphing calculator makes light piece of work of finding cut off points for a acme percent with the Changed Normal office. What you're really doing is looking for the cut off points for a certain percentile: for instance, if you take a list of grades and you want to know what score is at the 99th percentile, yous can use the inverse normal function to discover that percent cut-off point.

1. Finding Cut Off Points For a Meridian Percent

Sample problem: Students at a certain college average 5 anxiety viii inches (68 inches) tall. The heights are commonly distributed, with a standard departure of two.five inches. What is the value that separates the meridian one% of heights from the rest of the population?

Step 1: Press APPS and use the scroll keys to highlight Stats/List Editor.

Pace 2: Press F5 2 1 (this gets you lot to the Inverse Normal screen).

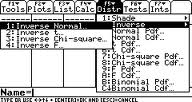
Step 3: Enter 0.99 in the Surface area box.

Step 4: Enter 68 in the μ box.

Stride v: Enter 2.5 in the σ box.

Step vi: Press ENTER.

Step 7: Read the results: Inverse=73.8159 means that the cut off top for the 99th percentile is 73.8159 inches.

That's information technology!

2. Probability Proportion Example (NormalCDF function)

Sample question: A group of students with commonly distributed salaries earn an average of $six,800 with a standard deviation of $2,500. What proportion of students earn between $half-dozen,500 and $7,300?

Stride 1: Press APPS. Scroll to the Stats/Listing Editor and press ENTER.

Step 2: Press F5 4.

Step iii: Enter 6500 in the lower value box.

Step four: Enter 7300 in the upper value box.

Step 5: Enter 6800 in the μ box.

Step 6: Enter 2500 in the σ box. Press ENTER.

Step 7: Read the answer. Cdf=.127018. In other words, .013, or thirteen% of students earn between $6,500 and $7,300.

TI-89 Graphing a Normal Distribution Curve

The TI-89 can not simply calculate z-scores and return values for normal distributions, it tin can graph the normal distribution curve besides. Graphing a normal distribution can help you see what it is you are supposed to exist looking for, and gives you 1 more tool in solving normal distribution problems. The TI-89 tin graph a normal distribution curve with an expanse shaded for any value. For example, you could create a graph that is: less than a certain number, greater than a certain number, or in-between a certain set of numbers.

Sample problem: Depict a normal distribution curve for student salaries during a typical semester. The student salaries have a hateful of $6,800 and standard difference of $2,500. Shade the area on the graph that corresponds to salaries between $vii,300 and $9,000.

Step 1: Printing APPS and select the Stats/List Editor.

Step ii: Press F2 3 and F2 4.

Stride three: Press F5 ) one.

Step 4: Scroll down and enter 7300 in the lower value box.

Step 5: Scroll downward and enter 9000 in the upper value box.

Pace half-dozen: Scroll down and enter 6800 in the μ box.

Step vii: Roll down and enter 2500 in the σ box.

Step eight: Ringlet downwards. Turn Auto Scale to "yes" past pressing the right curlicue fundamental, so the downwardly ringlet key to select yes. Printing ENTER.

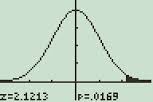
A normal distribution graph displayed on the TI-89 calculator.

That'due south information technology!

Tip: If you want to enter ∞ (infinity) as 1 of your lower or upper values, press the diamond fundamental and then Catalog.

Excel Graphing

Spotter the video for instructions on how to create a bell bend in Excel:

Can't see the video? Click hither.

Probability Density Role

• μ and σ are fixed constants.
• e¹⁰ = Exponential function (Kjos-Hanssen, 2022).

References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 533-534, 1987.
Feller, Westward. An Introduction to Probability Theory and Its Applications, Vol. ane, tertiary ed. New York: Wiley, 1968.
Kenney, J. F. and Keeping, Eastward. S. Mathematics of Statistics, Pt. 2, second ed. Princeton, NJ: Van Nostrand, 1951.
Kjos-Hanssen, B. (2019) Statistics for Calculus Students. Retrieved April 30, 2022 from: https://dspace.lib.hawaii.edu/handle/10790/4572

Kraitchik, Yard. "The Mistake Bend." §6.iv in Mathematical Recreations. New York: W. W. Norton, pp. 121-123, 1942.
Patel, J. K. and Read, C. B. Handbook of the Normal Distribution. New York: Dekker, 1982.

Related Manufactures

1. What is the 68-95-99.7 Dominion?
2. Box Cox Transformation
3. Box Muller Transform
4. Gaussian Mixture Models.
5. What is a Normal Probability Plot?
6. How to Calculate a Z-Score in Statistics
7. Find the area to the right of a z score.
8. Using the Normal Approximation to solve a Binomial Problem
9. What is the continuity correction factor?
10. Expanse Under a Normal Distribution Bend Index
11. Key Limit Theorem.
12. The Skew Normal Distribution.
13. 2 Tailed Normal Bend.
14. The Q Function.

---------------------------------------------------------------------------

Demand help with a homework or test question? With Chegg Report, you can get footstep-past-step solutions to your questions from an expert in the field. Your commencement xxx minutes with a Chegg tutor is gratis!

Comments? Need to mail service a correction? Delight post a comment on our Facebook page .

Source: https://www.statisticshowto.com/probability-and-statistics/normal-distributions/

Posted by: troupeingthe.blogspot.com

Share this post